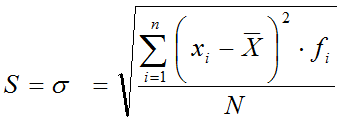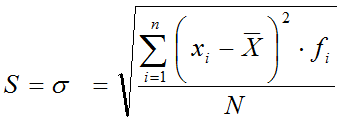MEDIDAS DE DESCRIPTIVAS
La medida descriptiva son valores numéricos calculados a partir de la muestra y que nos resume, la información contenida en ella.
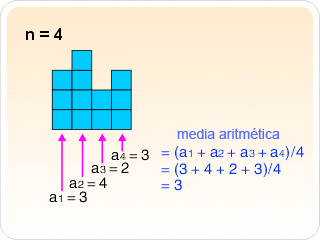
Medida o promedio aritmético
La medida de un conjunto de datos es la suma de las medidas divididas entre el numero total de datos.
Es el valor que separa por la mitad las observaciones ordenadas de menor a mayor, de tal forma que el 50% de estas son menores que la mediana y el otro 50% son mayores. Si el número de datos es impar la mediana será el valor central, si es par tomaremos como mediana la media aritmética de los dos valores centrales.
Dato central si son dos se saca la media de estos
(M0): es el valor de la variable que más veces se repite, es decir, aquella cuya frecuencia absoluta es mayor. No tiene porque ser única.
Dato que mas se repite si son dos es bimodal si son 3 es trimodal
EJEMPLO:
MEDIDAS CENTRALIZACIÓN
Las medidas de variabilidad nos ayudan a comprender la distribución de los datos es decir, el como están organizados, en congruencia siempre deben ir acompañadas de las medidas de tendencia central y de ubicación.Estas medidas son:
Rango o amplitud es el intervalo donde se encuentran los datos y están dado por r=x(max)-x(min).aunque cabe resaltar que no da mucha información con relación a la formación de datos
- Varianza y Desviación Estándar
Ahora bien la desviación estándar describe la distancia acumulada que tienen los datos a su medida y esta dad por la varianza es( el cuadrado de la desviación estándar)

Es una indicación relativa de la variación se expresa en porcentaje y es útil cuando se requiere comparar la dispersión de datos de dos o mas conjuntos de datos

MEDIDAS DE POSICIÓN
Si bien la mediana divide el conjunto de datos en dos partes iguales, existen otros parámetros estadísticos que dividen a la población en otras cuantías distintas.
Los cálculos son similares a los de la mediana, variando la posición a buscar y el intervalo en el que se encuentra el cuantil.
Los más importantes son los siguientes:
Dividen a la población de datos en cuatro partes iguales, correspondiendo cada uno de ellos al 25% de los datos. Tenemos por tanto tres cuartiles que denotamos como Q1, Q2, Q3, y se les llama primer, segundo y tercer cuartil.
El segundo cuartil coincide con la mediana.
Dividen la distribución de datos en 10 partes iguales, correspondiendo cada uno al 10% de los datos. Tendríamos, por tanto, nueve deciles que denotamos por D1, D2, D3, ..., D9
El quinto decil coincide con la mediana.
Tenemos 99 percentiles que dividirían a la población en 100 partes iguales, denotados por P1, P2, ..., P98, P99.
Los percentiles 25, 50 y 75 coinciden con los cuartiles.
MEDIDAS DE DISPERSIÓN
Las medidas de dispersión también llamada medidas de variabilidad muestran la variabilidad de una distribución indicando por medio de un numero si las diferentes puntuaciones de una variable están muy alejados de la media. Cuando mayor sea ese valor , mayor sera la variabilidad y cuanto menor sea mas homogénea sera a la media media así se saben si todos los casos son parecidos o varían mucho entre ellos
Es el recorrido estadístico que diferencia el valor máximo y el valor minino en un grupo de números aleatorios. El cual ordenamos los números según su tamaño y resta,os el valor mínimo del valor máximo
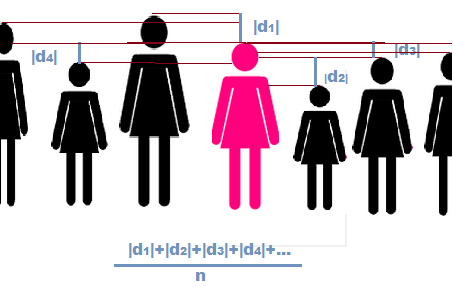
Como el parámetro de dispersión que sirve para calcular cuánto se desvían en promedio los datos de la distribución de la media aritmética. Se calcula como la media de los valores absolutos de las diferencias entre la media aritmética y los diferentes datos.
Es una medida estadística que mide la dispersión de los valores respecto a un valor central. una varianza es siempre positiva o 0
se le suma una cantidad constante a los datos de la distribución la varianza no se modifica
si los datos de la distribución los multiplicamos una contante la varianza queda multiplicada por el cuadrado de esa constante
La varianza viene dada por las mismas unidades que la variable pero al cuadrado, para evitar este problema podemos usar como medida de dispersión la desviación típica que se define como la raíz cuadrada positiva de la varianza.