Las medidas de dispersión están encaminadas a cuantificar lo próximos o alejados que están los datos de la muestra de un punto central.
Estas medidas indicaran por un lado el grado de variabilidad que hay en la muestra y, por otro, la representativo de dicho punto central, ya que sise obtiene un valor pequeño, eso significara que los valores se concentran entorno a ese centro por lo que habrá poca variabilidad y el centro representara bien a todos. En cambio, si se obtiene un valor grande, significara que los valores no están concentrados, sino dispersos por lo que habrá mucha variabilidad y el centro no sera muy representativo.Las medidas de dispersión reflejan la mayor o menor concentración con que se encuentran distribuidos los valores de la serie alrededor de un valor central.
Las principales medidas de dispersión son:
• Recorrido
• Desviación media
• Varianza
• Coeficiente de variación
- Recorrido
El rango es la diferencia entre el mayor y el menor de los datos de una distribución estadística.
Se define como la diferencia entre el último valor de la variable y el primero.
R = xM – xm
- Desviación media
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media
Consideramos la desviación de un valor de la variable como la diferencia en valor absoluto entre ese valor de la variable y la media aritmética de la serie.
- Desviación media para datos agrupados
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
La desviación media se representa por
- Varianza
La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.
- Coeficiente de variación
El coeficiente de variación es la relación entre la desviación típica de una muestra y su media.
Importancia para la carrera de Sistemas de la Información
Las medidas de dispersión indican la variación de los datos de una distribución, mostrando por medio de un valor, que tan alejados están los datos de un espacio muestra se puede utilizar en sistemas de información ya que esta enfocado con las operaciones y así poder hacer algún programa en cualquier programas . Conocer las medidas de dispersión permite saber si los datos son parecidos o tienen variaciones significativas pretende aportar al conocimiento un Software de Aplicación y se puede ser desarrollado con Lenguajes de programación , a fin de que contribuya con la obtención de resultados para datos no agrupados a través de Sistemas Computacional
Ejemplos de ejercicio
Ejemplo: En seis sábados consecutivos un operador de taxis recibió 9, 7, 11, 10, 13 y 7 llamadas a su sitio para su servicio. Calcule:
En este ejemplo tenemos principales medidas de dispersión ya que cada uno de ellos tienen formulas y casi poder calcular el resultado que deseamos obtener de cada uno
Que es varianza ?
La varianza de una variable aleatoria es una característica numérica que proporciona una idea de la dispersión de la variable aleatoria respecto de su esperanza. Decimos que es un parámetro de dispersión.La varianza y la desviación estándar son medidas de dispersión o variabilidad, es decir, indican la dispersión o separación de un conjunto de datos. Hay que tener en cuenta que las fórmulas de la varianza y la desviación estándar son diferentes para una muestra que para una población.
Propiedades de varianza
Algunas propiedades de la varianza son:
Var(X) ≥ 0
- Var(k · X) = k2 · Var (X) para todo numero real k.
Var(k) = 0 para todo numero real k.
Var(a · X + b) = a2 · Var(X) para todo par de números reales a i b.
Var(X + Y) = Var(X) + Var(Y) únicamente en el caso que X y Y sean independientes
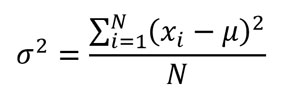
Desviación estándar de la población (σ)
La desviación estándar de la población es simplemente la raíz cuadrada de la varianza de la población. Como la varianza es el promedio de las distancias al cuadrado que van desde las observaciones a la media, la desviación estándar es la raíz cuadrada del promedio de las distancias al cuadrado que van desde las observaciones a la media. La desviación estándar está en las mismas unidades que las que se usaron para medir los datos. La raíz cuadrada de un número positivo puede ser tanto positiva como negativa. Cuando tomamos la raíz cuadrada de la varianza para calcular la desviación estándar, los estadísticos solamente consideran la raíz cuadrada positiva.
La desviación estándar es la raíz cuadrada positiva de la varienza
Varianza de la muestra (s2)
La fórmula de la varianza de la muestra es diferente a la de varianza de la población.
Desviación
estándar de la muestra (s)
Recuerda que la desviación
estándar es la raíz cuadrada positiva de la varianza.
EJEMPLO
Hallar la desviación
media, la varianza y la desviación típica de la series de
números siguientes:
a) 2,3,6,8,11
b) 12,6,7,3,15,10,18,5
El coeficiente de variación es una medida de dispersión
relativa (libre de unidades de medida), que se define como el cociente de la
desviación estándar entre la media aritmética. En esta clase, veremos cómo
calcular su valor y también su utilidad.
El coeficiente
de variación es la relación entre la desviación típica de una muestra y su media.
El coeficiente de variación se suele expresar en
porcentajes
El coeficiente de variación permite comparar las
dispersiones de dos distribuciones distintas, siempre que sus medias sean
positivas.Se calcula para cada una de las distribuciones y los valores
que se obtienen se comparan entre sí.
Propiedades
estadísticas coeficiente de desviación estándar
- El coeficiente de variación es típica mente menor que uno.
- Para su mejor interpretación se lo
expresa como porcentaje.
- Depende de la desviación típica y en mayor
medida de la media aritmética, dado que cuando esta es 0 o muy próxima a este
valor C.V. pierde significado, ya que puede dar valores muy grandes, que no
necesariamente implican dispersión de datos.
- El coeficiente de variación es
común en varios campos de la probabilidad aplicación
EjemploEn seis sábados consecutivos un operador de taxis recibió 9, 7, 11, 10, 13 y 7 llamadas a su sitio para su servicioEn este ejemplo de este ejercicio lo primero debemos calcular media mediadas amplitudes o rangos y calcular la desviación media desviación entandar y varianza cada uno tiene distintos formulas con ese podemos obtener el resultado de cada uno y también para poder obtener el resultado de la coeficiente de variacion
El coeficiente de variación es una medida de dispersión relativa (libre de unidades de medida), que se define como el cociente de la desviación estándar entre la media aritmética. En esta clase, veremos cómo calcular su valor y también su utilidad.
El coeficiente de variación se suele expresar en porcentajes
El coeficiente de variación permite comparar las dispersiones de dos distribuciones distintas, siempre que sus medias sean positivas.Se calcula para cada una de las distribuciones y los valores que se obtienen se comparan entre sí.
Propiedades estadísticas coeficiente de desviación estándar
- El coeficiente de variación es típica mente menor que uno.
- Para su mejor interpretación se lo expresa como porcentaje.
- Depende de la desviación típica y en mayor medida de la media aritmética, dado que cuando esta es 0 o muy próxima a este valor C.V. pierde significado, ya que puede dar valores muy grandes, que no necesariamente implican dispersión de datos.
- El coeficiente de variación es común en varios campos de la probabilidad aplicación
No hay comentarios:
Publicar un comentario